Textual representatin of Pitch Class (PC) and Pitch Class Set (PCS)
We have a preferenc for integer notation as PC (pitch class), because it eliminates any ambiguity (no enharmonic notation such that A = Bbb = G ## …), but we do not prohibit the use of solfege-latin notation neither.
| Integer PC | solfege PC | pitches |
|---|---|---|
| 0 | C | C0, C1, … |
| 1 | C#, Db, … | C#0, C#1, Db1, … |
| 2 | D, Ebb, … | D0, D1, … |
| 3 | D#, Eb, … | D#0, D#1, … |
| 4 | E, Fb, … | E0, E1, … |
| 5 | F, E#, … | F0, F1, … |
| 6 | F#, Gb, … | F#0, F#1, … |
| 7 | G, Abb, … | G0, G1, … |
| 8 | G#, Ab, … | G#0, G#1, … |
| 9 | A, Bbb, … | A0, A1, … |
| 10 | A#, Bb, … | A#0, A#1, … |
| 11 | B, Cb, … | B0, B1, … |
A PCS is a subset of {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} (Although its elements are not ordered by definition, it is usual to present them in ascending order to facilitate their reading)
Examples :
- Empty set :
{ }; - DO-DO#-RE :
{0, 1, 2} - DO-RE-MI :
{0, 2, 4} - C7 :
{0, 4, 5, 7} - G7 :
{2, 5, 7, 11} - Chromatic :
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
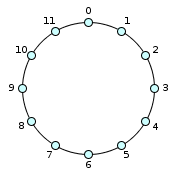
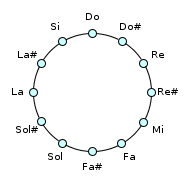
Circular representation of 12 Pitch Class
Example of circles with labels :
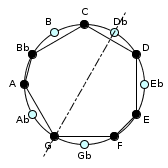
Examples of Pitch Class Set (PCS) representation

{0, 2, 4, 5, 7, 9, 11}
{0, 2, 4, 5, 7, 9, 10}
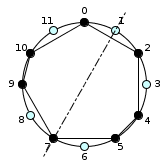
{0, 2, 4, 5, 7, 9, 10}

{0, 2, 4, 6, 7, 9, 11}
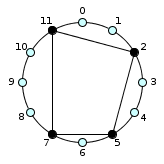
{2, 5, 7, 11}
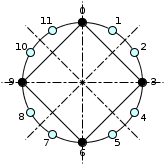
{0, 3, 6, 9}
Interests of circular representation
As you can see, the circular representation, much more than text, makes it possible to put forward symmetries and characteristic structures, some of which are easily detectable such as regular polygons and their relationship (but not always) with limited transposition structures.
Intervallic struture by illustration
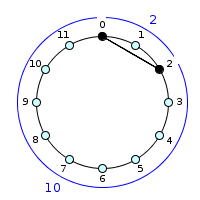
is : (2, 10)
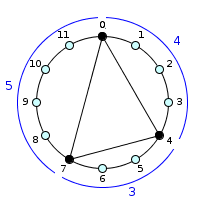
is : (4, 3, 5)
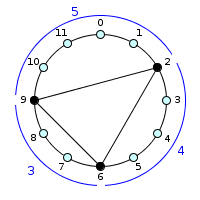
is : (4, 3, 5)
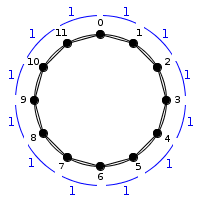
is : (1,1,1,1,1,1,1,1,1,1,1,1)
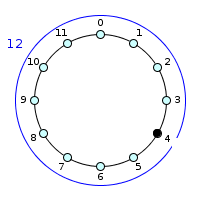
is : (0) - or (12)

is : () - empty list
References and Co
-
Constellation vs Polygon : another approach to form in a chromatic circle
-
As early as 1679, design circle 7 step