Matrix instrument
As regular tuning instrument, a matrix instrument is instance of a dual interval space (DIS), as two-dimentional array of pitches where “rows” are separated by the same interval, the “columns” (non-zero) interval.
Matrix instrument can be noted as follows: DIS(y,x) where y is row interval and x is culumn interval.
violin

DIS(2,3)
accordion (right hand)
Rem : for a formal definition of DIS see Dual Interval Space in Twentieth-Century Music, Stephen C.Brown.
Case of strings instruments
Strings instruments are always tuning with interval 1 (row interval - to play along the string) and an other that varies. For example, violin is (1, 7), and it is said tuned in fifths (fifth is composed of 7 semitones), bass (1, 5) and it is said tuned in fourths. Traditionnal violin has 4 strings, bass has 3, 4 or 5 strings, and same interval is kept between the neighboring strings. This is referred to as regular tuning.
Of course there is the guitar tuned in fourths (and this may be why you read these lines), but also instruments in regular tuning, as (1,4) major 3rd, for example.
Remarkable tunings
It would seem (but it remains to prove) that the choose a DIS with 2 generators of 12 (one for each dimension of the matrix), gives the latter interesting properties.
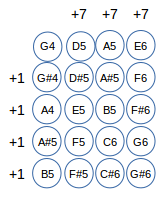
The 4 generators of 12 {1, 5, 7, 11} – or more conceptualy {1, 5, n-5, n-1 } with n=12, can be supported by 2 axes and so 4 angulars sectors : 1-O-5, 7-O-1, 7-O-11 and 11-O-5, as showing with figure below :
A angular sector forms a two-dimensional array (DIS), Below, we choose as origin 0, elements are pitches in scientific pitch notation.
This space can be considered as a musical keyboard. Like keyboard of piano, let us emphasize the notes of diatonic scale.
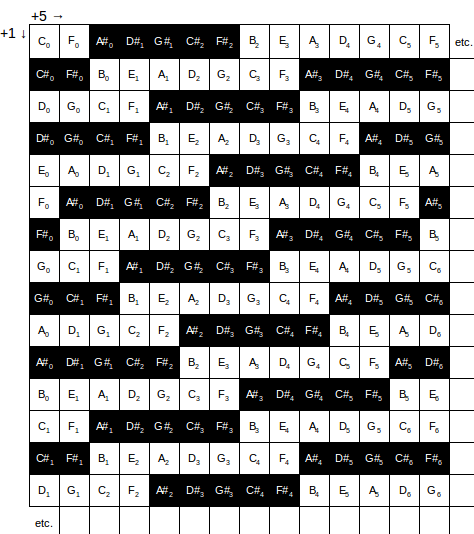
C-diatonic
(2, 2, 1, 2, 2, 2, 1)
{C, D, E, F, G, A, B}
The motif that emerges from this representation (  ) is the very basis of the 88 musaics: their nature is geometrical.
) is the very basis of the 88 musaics: their nature is geometrical.
Diatonic tones shape in DIS(1,5)
Let’s take a look at F diatonic tonality :

{C, D, E, F, G, A, Bb}
(2, 2, 1, 2, 2, 2, 1)

{0, 2, 4, 5, 7, 9, 10}
(2, 2, 1, 2, 2, 2, 1)
Recognizable shapes
With this system of representation, each harmonic color is associated with one and only one form, as a marker.
We can even remove the labels to better emphasize the shape.
Would you recognize the diatonic intervallic structure form (2, 2, 1, 2, 2, 2, 1) ? :
 |
 |
 |
 |
 |
 |
… We think you did. There are four : 1, 2, 3 and 6. Each time, it is the same pattern used to select the diatonic form.
Examples :

By definition, all diatonic scales are same intervallic structure (2, 2, 1, 2, 2, 2, 1) that may be represented by a graphic motif, invariant by transposition.

in DIS(1,5)
In fact, both ... because there no reason, a priori, to privilege one in relation to the other (its complementary)


in DIS(1,5)
Thus, as will be appreciated, such a pattern is the expression of two intervallic structures, mutually complementary, each of which can be realized by, at most, 12 different PCS (here, pentatonic and diatonic scales in 12 tones - 2 scales that have marked the history of music…)
How many distincts “motif patterns” are they in an octave of 12 equal semitones?
The answer depends on the intensity of the reduction : following this link : 88-musaics.org
Regular instrument
String instrument
Most stringed instruments are structured by a logical system: the contiguous strings are separated by the same interval, without exception.
The majority of stringed instruments is in regular tuning : violins (7-7-7-7), bass (5-5-5-5)… But this is not the case of the traditional guitar tuning that is (in semitone): 5-5-5-5-4-5, unlike the guitar in fourths: 5-5-5-5-5-5
trouble in translation
keyboard instrument
Regular tuning does not always rhyme with uniform interface … Indeed, the piano is a hybride regular instrument to the extent that its interface is “chromatic shape logic” at the bottom of the keyboard keys, and “C diatonic shape” in the foreground of keyboard keys where the distance between a white key and its neighbor is, depending on the case, either 2 semitones or 1 semitone : Thus the correspondence between geometric distance and interval distance is broken.

See new keyboard (symmetrical piano) : symmetrical-ui keyboard
win instrument
Few regular interface in this range of acoustic instruments
TODO
Linear instrument
Util minimum for musical instrument is to take one generator, more often genrator 1.
For example, mono string instrument.
or piano.