Introduction
This study falls within the simplified framework of the 12 equal temperament (which divides the octave into twelve “equal” parts)
Nothing new, is the case of the main musical instruments with prepared notes (fretted instruments, piano, synthesizer, …)
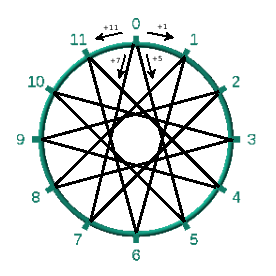
Generators of 12
Chromatic scale can be generated in 4 ways (4 integers where are prime form with 12):
- step 1 : C0, C#0, D0, D#0, E0, F0, F#0, G0, G#0, A0, A#0, B0, C1, C#1, etc.
- Case of string instrument, piano keyboard
- step 5 : C0, F0, Bb0, Eb1, Ab1, Db2, Gb2, B2, E3, A3, D4, G4, C5, F5, etc. (rem : Bb ~ A# ~ Cbb …)
- Conjugated with the first (step 1), case of string instruments tuning in fourths (guitar, bass, bajosexto, …)
- step 7 : C0, G0, D1, A1, E2, B2, F#3, C#4, G#4, D#5, A#5, F6, C7, G7, etc.
- Conjugated with the first (step 1), case of string instruments tuning in firths (mandolin, violin, cello, …)
- step 11 : C0, B0, A#1, A2, G#3, G4, F#5, F6, E7, D#8, D9, C#10, C11, B11, etc.
- ? no case ?
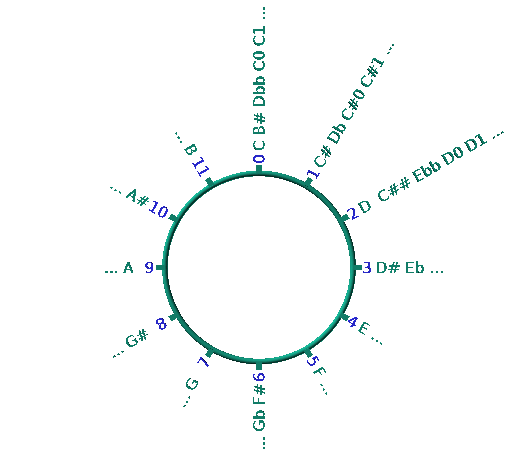
Enharmonic equivalence
Enharmonic equivalence is a pragmatic axiom that unifies close pitches such as C4, B3#, D4bb …
It is on this principle that, today, many user interfaces (UI) of musical instrument are designed (keyboard piano, guitar frets, …).
Octave equivalence
Octave equivalence is manifested by the fact we spell different pitches by the same name, whatever this frequency, on condition that are on octave rapport.
For example, there are different sounds such as C4, C5, C6, but only one equivalence class named C.
- C0, C5, …, Cn are pitches
- C is Pitch Class in Musical Set Theory terminology, noted most often 0 (zero).
It is well known by the musician for the notation of chords: CMaj7 designates all the chords, with a Cx as root, based on a structure (4, 3, 4, 1) ie 3rd maj, fifth and major seventh.
(with integer notation)
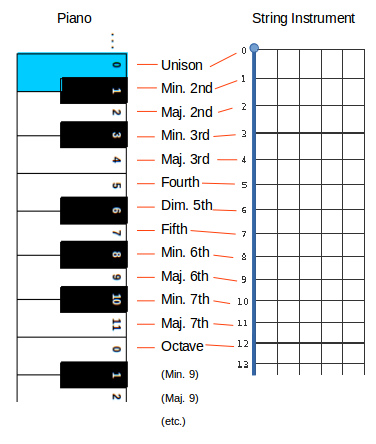
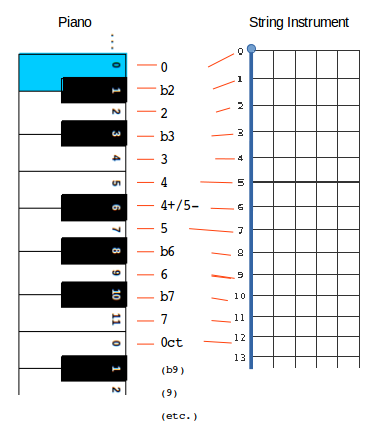
Intervals within octave
This study makes intensive use of interval.
An interval is the “distance” in semitone between 2 PCs (the number of semitones separating 2 notes).
Each interval has a name (or even several if we ignore enharmonic identification) resulting from tonal analys which is based on 7 notes and not 12… This results in a naming not always logical, a priori: fifth = 7, third major = 4, etc.
Here is a table of intervlas common names, from PC = 0 :
P vs PC vs PCS
-
Pitch refers to height of sound, frequency (example :
A4) -
Pitch Class (PC) refers to height class, octave equivalence is applied (example :
Aor9- in numeric notation) -
Pitch Class Set (PCS) refers to a set of pitch classes, without duplicate element (example :
{C, E, G}or{0, 4, 7}) - ordered by convention
PC interval
Interval is a distance between two pitches, measured in semitones. It may be null (unison), ascending or descending.
But this traditional perception can not be applied to PCs, because of the octave equivalence which cancels orientation. Indeed, {0, 2} can be the expression of both a second and a seventh, therefore of an interval and its inversion.
Intervallic Structure (IS)
What characterizes a chord color, a scale, a mode? It is both the number of notes that compose them (cardinal) and distance between these notes (interval). For example, a minor 7 chord is characterized by both a analytical notation from root (minor third, fifth, minor seventh - or b3,5,b7) or successive intervals (3, 4, 3, 2) as shown below :
Example : Minor seventh structure chord :
roottob3= 3 semitonesb3to5= 4 semitones5tob7= 3 semitonesb7toroot= 2 semitones
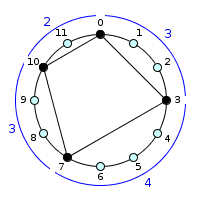
is : (3,4,3,2)
So, (3,4,3,2) is the marker of all minor 7 chords, is intervallic structure of minor7 (r,b3,5,b7).
These two representations of a PCS structure (successive intervalls or intervalls from root) are equivalent.
Def : Intervallic Structure (is) is a function that, when applied to a PCS, returns, in an ordered collection of intervals that constitute it.
The sum x of these intervals always verify that x is multiple of 12.
Examples :
is({0,2})return(2,10)because 0-2 is major second interval (2 semitones) and 2-12 interval is de Minor 7 (10 semitones). 10 + 2 = 12, ok.is({0, 4, 7})return(4,3,5)(major third, minor third, fourth)is({1, 5, 8})return(4,3,5)(major third, minor third, fourth)is({4})return(0)* rem: 12 is equivalent to 0 with octave identification *is({6})return(0)is({0,1,2,3,4,5,6,7,8,9,10,11})return(1,1,1,1,1,1,1,1,1,1,1,1)
Equivalent Class of Structure - Cyclic Group
We can group the PCS having the same interval structure (352 classes)
PCS-Class
Grouping criteria (PCStrivial, PCSCyclic, Dihedral, Affine, Musaic,… )
PCS-Class and Prime Form
Prime Forme is minimal PCS of this PCS-Classe (minimal element of class)
=> See with circle representation
References and Co
Musical Set Theory